
7453번: 합이 0인 네 정수
첫째 줄에 배열의 크기 n (1 ≤ n ≤ 4000)이 주어진다. 다음 n개 줄에는 A, B, C, D에 포함되는 정수가 공백으로 구분되어져서 주어진다. 배열에 들어있는 정수의 절댓값은 최대 228이다.
www.acmicpc.net
문제
정수로 이루어진 크기가 같은 배열 A, B, C, D가 있다.
A[a], B[b], C[c], D[d]의 합이 0인 (a, b, c, d) 쌍의 개수를 구하는 프로그램을 작성하시오.
문제 접근
A[a] + B[b] + C[c] + D[d] = 0 이 성립하는 {a, b, c, d}의 개수를 구하라.
첫 번째 방법입니다.
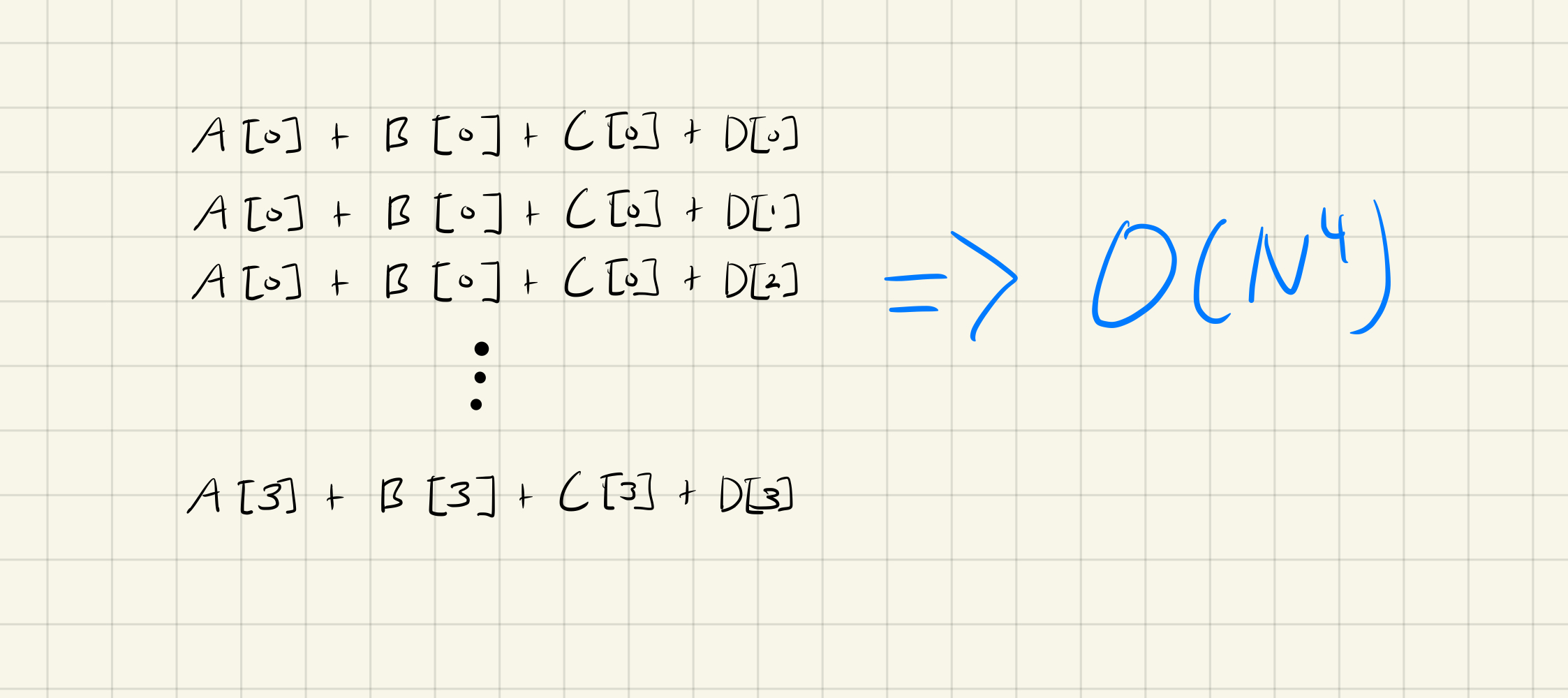
위와 같이 무작정 더하는 방법인데 O(n^4)는 좀 아니지 않나 싶습니다.
두 번째 방법입니다.
이번에는 이분 탐색 방법을 적용해보려고 합니다.
AB배열과 CD배열을 만들고 정렬합니다.
포인터 p1, p2를 배치합니다.
이후 p1, p2를 움직이며 AB[p1] + CD[p2] == 0 일 경우를 찾습니다.
AB[], CD[] 를 만드는데 N^2 * 2
AB[], CD[] 를 정렬하는데
AB[]는 N^2개의 원소이므로 -> (N^2)log(N^2)이다.
즉, 4N^2log2
포인터 움직이는데 최대 N + N
-> O(N^2logN) 이 됩니다.

주의 해야할 점
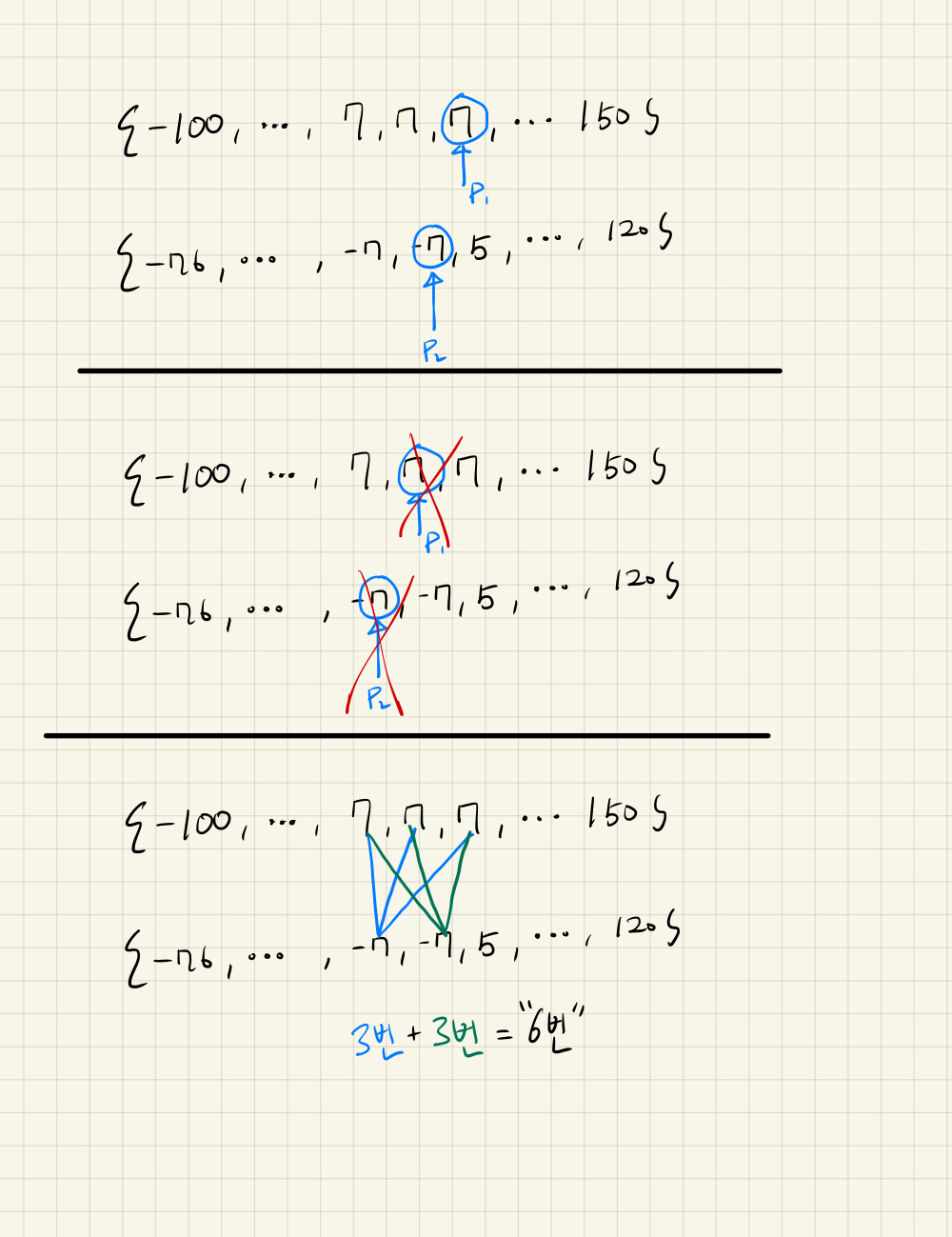
동률 처리
동률 처리를 해줘야 합니다.
AB[] 와 CD[]내에 중복이 없다면 상관없지만 중복이 있을 시에 p1, p2가 제대로 처리 해주지 못합니다.
때문에 AB[p1] + CD[p2] == 0 일 때
AB[p2]이 AB 내에 몇 개 있는지
CD[p2]가 CD 내에 몇 개 있는지 확인해서 처리해줘야 합니다.
아래 그림과 같이
AB 내에 ‘7’이 3개
CD 내에 ‘-7’이 2개 존재하다면
3 * 2 = 6개 될 수 있습니다.
long
AB[], CD[]에 들어갈 원소의 값은 int형으로 감당할 수 있지만
(p1, p2) 의 쌍은 최대 N^2 * N^2 입니다.
N^4은 최대 1600만^2 입니다.
때문에 쌍의 개수를 저장할 answer과 동률이 최대 1600만^2개 있을 수 있으므로
long 동률Count
long answer
으로 선언해서 사용해야 합니다.
내 코드
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
final int N = Integer.parseInt(br.readLine());
final int M = 4;
int[][] arr = new int[M][N * N];
int[] AB = new int[N * N];
int[] CD = new int[N * N];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < M; j++) {
arr[j][i] = Integer.parseInt(st.nextToken());
}
}
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
AB[count] = arr[0][i] + arr[1][j];
CD[count++] = arr[2][i] + arr[3][j];
}
}
Arrays.sort(AB);
Arrays.sort(CD);
long answer = 0;
int p1 = 0;
int p2 = count - 1;
while (p1 < count && p2 >= 0) {
if (AB[p1] + CD[p2] < 0) {
p1++;
} else if (AB[p1] + CD[p2] > 0) {
p2--;
} else {
// 동률을 구한다
long p1Count = 0;
long p2Count = 0;
int p1Original = p1;
while (AB[p1] + CD[p2] == 0) {
// 현재에 대한 동률 개수 = + 1
p1Count++;
// 다음으로 찾을 인덱스 = p1 + 1
p1++;
if (p1 >= count) {
break;
}
}
while (AB[p1Original] + CD[p2] == 0) {
p2Count++;
p2--;
if (p2 < 0) {
break;
}
}
answer += p1Count * p2Count;
}
}
System.out.println(answer);
}
}'PS > 백준' 카테고리의 다른 글
| [백준 with Java] 11559번 : Puyo Puyo - 시뮬레이션 (0) | 2022.08.11 |
|---|---|
| [백준] 3005번 - 탈출 (0) | 2022.07.19 |
| [백준] 1062번 - 가르침 (0) | 2022.07.19 |


댓글