
3176번: 도로 네트워크
첫째 줄에 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N-1개 줄에는 도로를 나타내는 세 정수 A, B, C가 주어진다. A와 B사이에 길이가 C인 도로가 있다는 뜻이다. 도로의 길이는 1,000,000보다 작거나 같은 양
www.acmicpc.net
문제
N개의 도시와 그 도시를 연결하는 N-1개의 도로로 이루어진 도로 네트워크가 있다.
모든 도시의 쌍에는 그 도시를 연결하는 유일한 경로가 있고, 각 도로의 길이는 입력으로 주어진다.
총 K개의 도시 쌍이 주어진다. 이때, 두 도시를 연결하는 경로 상에서 가장 짧은 도로의 길이와 가장 긴 도로의 길이를 구하는 프로그램을 작성하시오.
문제 예측
문제를 보면 도로가 N - 1개로 유일한 간선에 사이클이 없음을 알 수 있습니다.
요구하는 것은 두 도시가 연결되는 최소 간선들로 min, max 를 구하라는 것이었습니다.
두 도시를 연결하기 위해서는 공통된 조상이 필요할 것이고 바로 LCA 혹은 DisjointSet으로 풀어야겠다고 생각했습니다.
입력과 시간 복잡도, min, max에 어떻게 대처해야할지 좀 더 생각해보고 알고리즘 결정을 하겠습니다.
시간 복잡도 알아보기
2 ≤ 도시 N ≤ 100,000
간선 N - 1
구해야할 두 정점의 min, max라 했을 때 두 정점이 주어지는 개수 K
1 ≤ K ≤ 100,000
두 정점 주어졌을 때
완전 탐색으로 찾는다고 하면 N - 1개의 간선을 확인해야 합니다.
근데 이 작업을 K번해야 하니
최악의 경우는
99,999 * 100,000 이며 대략 10억 정도의 연산으로 1초로는 어림도 없음을 알 수 있습니다.
빅오로 표기한다면 O(NK)입니다.
그렇다면 한 쪽을 O(1) 혹은 O(logN)만 맞춰주어도 맞출 수 있겠습니다.
문제 접근 1 : 두 도시 연결 → 최소 공통 조상 (LCA)
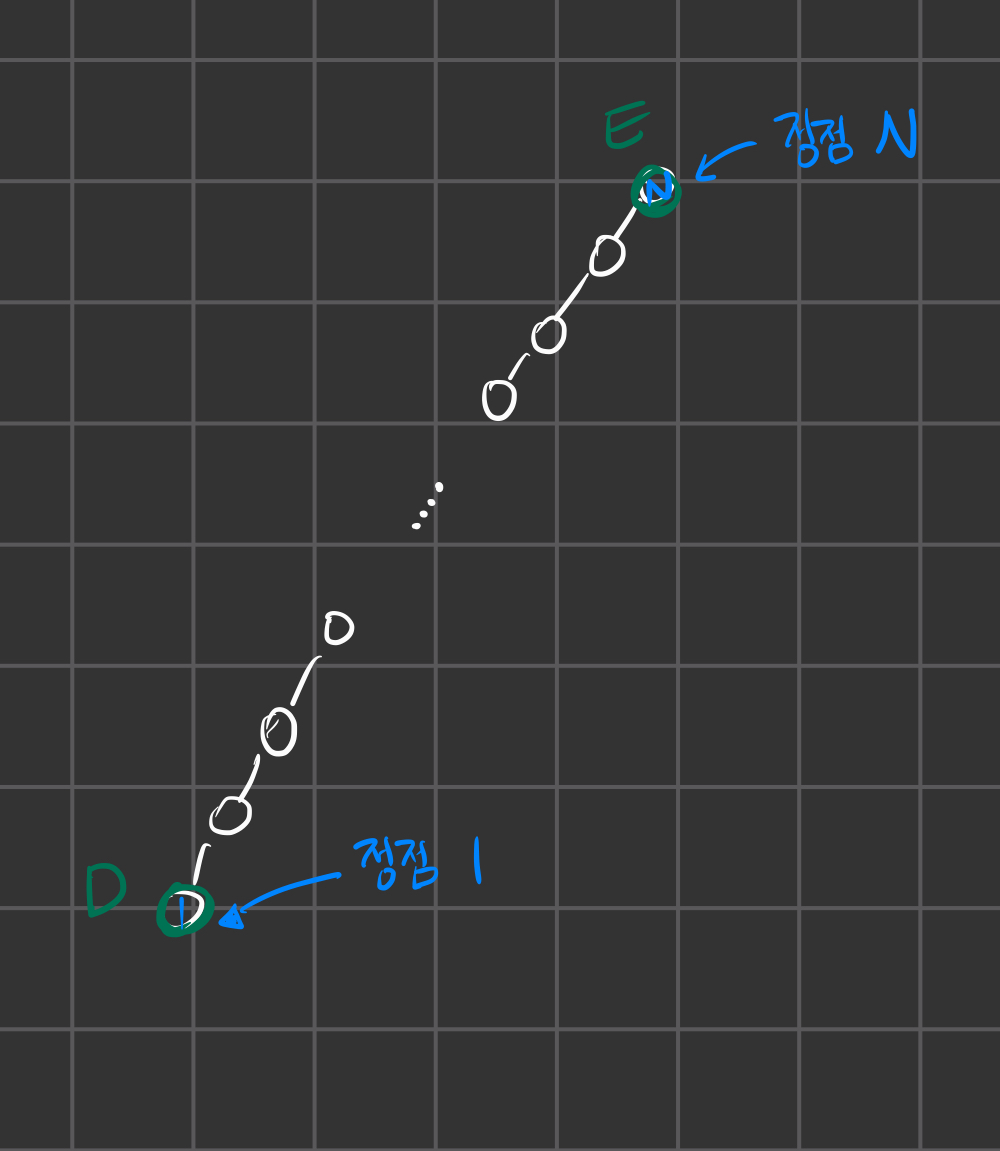
문제에서 두 도시 D, E가 주어졌을 때 두 도시를 연결하는 간선들중 거리의 min, max를 구하라고 하였습니다.
두 도시를 연결하기 위해서는 또 다른 도시 혹은 자기 자신이 필요합니다.
가장 가까운 공통되는 도시는 즉 최소 공통 조상을 의미하니 LCA로 두 도시 (D, E)의 최소 공통 조상을 찾고 그 때 연결된 각 간선의 min, max를 찾기로 결정했습니다.
문제 접근 2 : min, max 해결
먼저 완전 탐색을 한다고 했을 때 min ,max를 계속가지고 다니며 간선을 비교하기에는 너무나 큰 비용이 듭니다.
때문에 우리가 탐색하면서 가지고 다니기 위해서 비용을 줄이거나 다른 방법을 채택하려 합니다.
무슨 방법이 있을까 생각해보다가 LCA로 두 도시의 공통을 찾는거라면 두 도시의 min, max도 찾는 것이 가장 최적의 방법이라고 생각했습니다.
그렇다면 어떻게 해야지 min, max를 LCA를 응용하여 해결 할 수 있을까요?
먼저 LCA를 구현하기 위해서는 저희는 아래와 같은 두 배열이 필요했습니다.
int[] depth;
int[][] parent;
이 때 depth는 단어 그대로 각 도시의 깊이를 의미합니다.
parent배열은 parent[k][v]라고 했을 때 정점 v의 2^k번 째 조상을 가지는 2차원 배열이었습니다.
parent 2차원 배열이 왜 LCA를 구할 때 필요한지 이해하고 계셔야 이 문제에 접근하기 좋았습니다.
아래 포스팅에서 LCA를 잠시 보고 오셔도 좋을거 같습니다.
[알고리즘 특강 6일차] 서로소 집합, 위상정렬, 최소 신장 트리, 최소 공통 조상 (Disjoint Set, Union-Fi
최소 신장 트리 (MST; Minimum Spanning Tree) 트리란? (Tree) 무향 그래프 G가 순환 없는 연결 그래프이면 G는 트리입니다. 숲이란? (Forest) 무향 그래프 G가 순환이 없는 그래프이면 G는 숲입니다. 신장 트리
always-dev.tistory.com
다시 본론으로 들어가겠습니다.
만약 min, max도 LCA를 이용한다고 하면 parent와 같은 2차원 배열이 필요할 것입니다.
곧바로 아래와 같이 min, max를 위한 2차원 배열이 있다고 생각해봅시다.
int[][] minRoad;
int[][] maxRoad;
그렇다면 두 2차원 배열는 어떤 의미를 가질까요?
minRoad와 maxRoad는 다음과 같습니다.
- minRoad[k][v] : 정점 v의 $2^k$ 번 째 조상의 min 값
- maxRoad[k][v] : 정점 v의 $2^k$ 번 째 조상의 max 값
뭔가 될거 같은 느낌이 들지 않나요?
저는 여기서 좀 더 내용을 붙여가며 생각해보았습니다.
먼저 k에 0을 대입해서 생각했습니다.
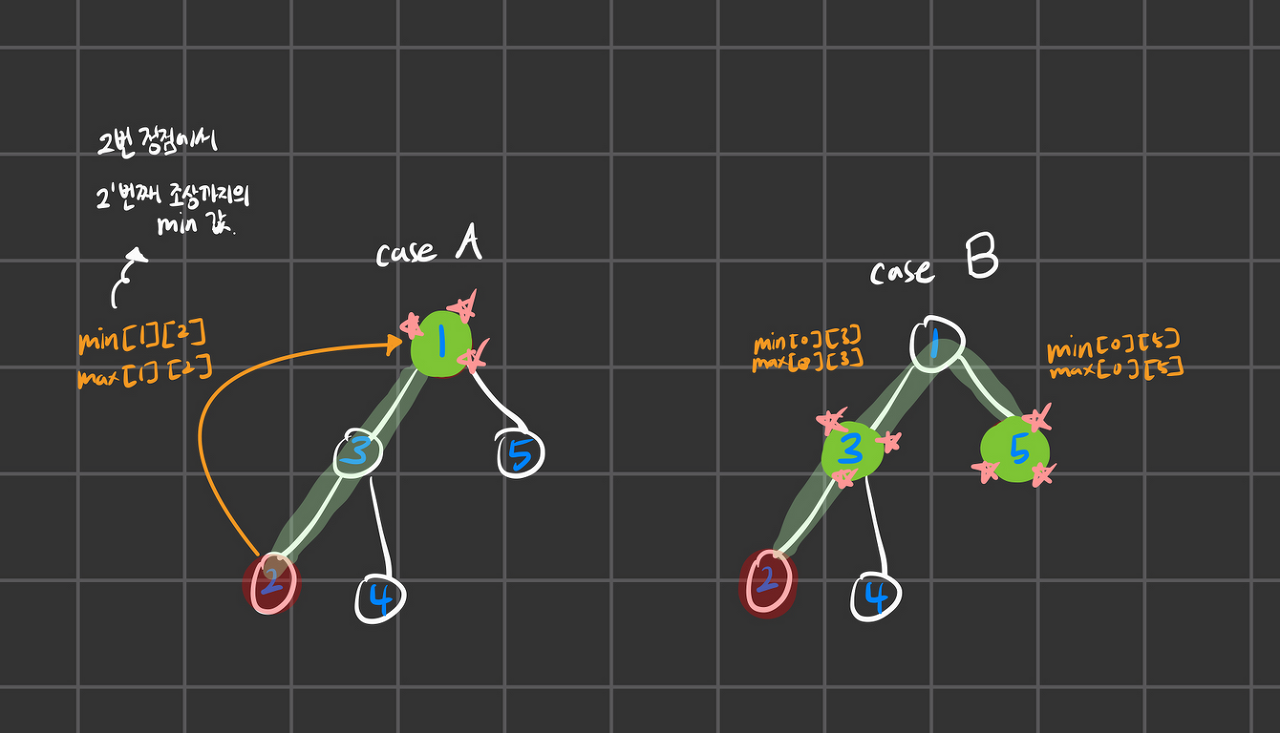
- minRoad[0][v] : 정점 v의 첫번째 조상의 min 값
- maxRoad[0][v] : 정점 v의 첫번째 조상의 max 값
오 이렇게 된다면 최소 공통 조상의 바로 직전 도시 들이 v라면 최소 공통 조상에 연결 됐을 때의 min, max를 구할 수 있습니다.
여기서 이것이 맞는가 검증하기 위해서 몇 가지 경우를 그려보면서 비교해보았습니다.
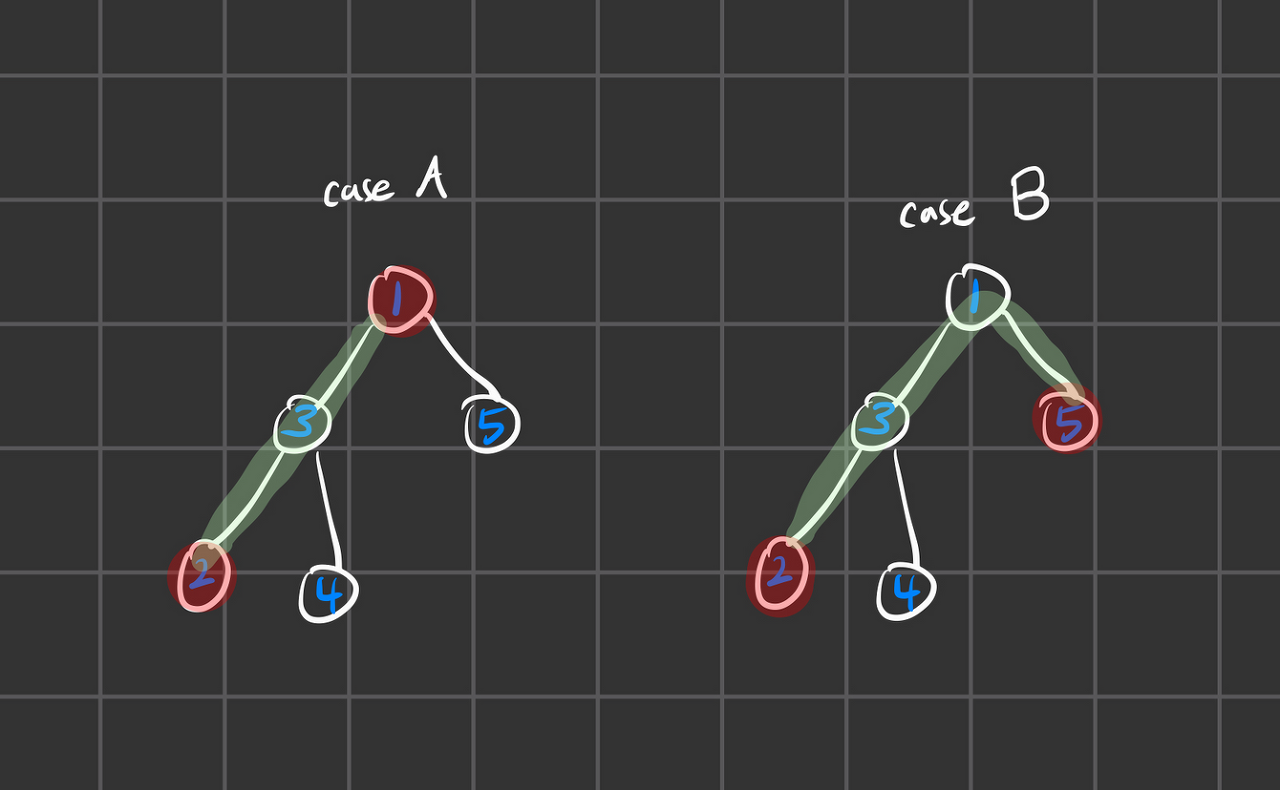
case A : 도시 1, 도시 2
case B : 도시 2, 도시 5
A, B 케이스를 보면 둘 다 최소 공통 조상이 1입니다.
그렇다면 min, max를 구할 때 둘이 똑같은 값이 나올까요 ?
그건 아닙니다.
왜냐하면 저희는 구한 최소 공통 조상 바로 직전의 도시들을 return 할 것이기 때문입니다.
또한 한번에 조상을 찾을 수 있을 때는 바로 구할 수도 있습니다.
도로 네트워크 코드 구현
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int N, K;
static int A, B, W;
static int D;
static List<Route> adj[];
static int[][] parentLCA;
static int[][] MAX_ROAD, MIN_ROAD;
static int[] depth;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
for (; (1 << D) < N; D++) ;
parentLCA = new int[D][N + 1];
MAX_ROAD = new int[D][N + 1];
MIN_ROAD = new int[D][N + 1];
depth = new int[N + 1];
adj = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) {
adj[i] = new ArrayList<>();
}
for (int i = 1; i < N; i++) {
st = new StringTokenizer(br.readLine());
A = Integer.parseInt(st.nextToken());
B = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
adj[A].add(new Route(B, W));
adj[B].add(new Route(A, W));
}
init();
makeParent();
K = Integer.parseInt(br.readLine());
for (int i = 0; i < K; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int[] answer = lca(u, v);
System.out.println(answer[0] + " " + answer[1]);
}
}
static int[] lca(int u, int v) {
int minRoad = Integer.MAX_VALUE;
int maxRoad = Integer.MIN_VALUE;
if (depth[u] < depth[v]) {
int temp = u;
u = v;
v = temp;
}
int gap = depth[u] - depth[v];
for (int i = 0; i <= D; i++) {
if (((gap & (1 << i)) > 0)) {
minRoad = Math.min(minRoad, MIN_ROAD[i][u]);
maxRoad = Math.max(maxRoad, MAX_ROAD[i][u]);
u = parentLCA[i][u];
}
}
if (u != v) {
for (int i = D - 1; i >= 0; i--) {
int findU = parentLCA[i][u];
int findV = parentLCA[i][v];
if (findU != findV) {
minRoad = Math.min(minRoad, Math.min(MIN_ROAD[i][u], MIN_ROAD[i][v]));
maxRoad = Math.max(maxRoad, Math.max(MAX_ROAD[i][u], MAX_ROAD[i][v]));
u = findU;
v = findV;
}
}
minRoad = Math.min(minRoad, Math.min(MIN_ROAD[0][u], MIN_ROAD[0][v]));
maxRoad = Math.max(maxRoad, Math.max(MAX_ROAD[0][u], MAX_ROAD[0][v]));
}
return new int[]{minRoad, maxRoad};
}
static void makeParent() {
for (int i = 1; i < D; i++) {
for (int j = 1; j <= N; j++) {
parentLCA[i][j] = parentLCA[i - 1][parentLCA[i - 1][j]];
MIN_ROAD[i][j] = Math.min(MIN_ROAD[i - 1][j], MIN_ROAD[i - 1][parentLCA[i - 1][j]]);
MAX_ROAD[i][j] = Math.max(MAX_ROAD[i - 1][j], MAX_ROAD[i - 1][parentLCA[i - 1][j]]);
}
}
}
static void init() {
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
depth[1] = 1;
while (!queue.isEmpty()) {
int curr = queue.poll();
for (Route next : adj[curr]) {
if (depth[next.b] > 0) continue;
MAX_ROAD[0][next.b] = next.w;
MIN_ROAD[0][next.b] = next.w;
depth[next.b] = depth[curr] + 1;
parentLCA[0][next.b] = curr;
queue.add(next.b);
}
}
}
}
class Route {
int b, w;
public Route(int b, int w) {
this.b = b;
this.w = w;
}
}


댓글